前言

在上一篇中，我们读到了感知机的数学建模原理，并用一组案例做了演示，最后稍微提到了它的局限性。这次课件中也会以图文的方式分析这种局限性，并引入第一种神经网络模型——前馈神经网络（Feedforward Neural Network）。

本文还是以翻译PPT页内容为主，打星号的部分则是我的补充说明。

1 神经网络的动机：需要非线性模型——Motivation for neural networks: need non-linear models

*这部分内容在上一篇的结尾简单的提到过，这次对照课件再来过一下。

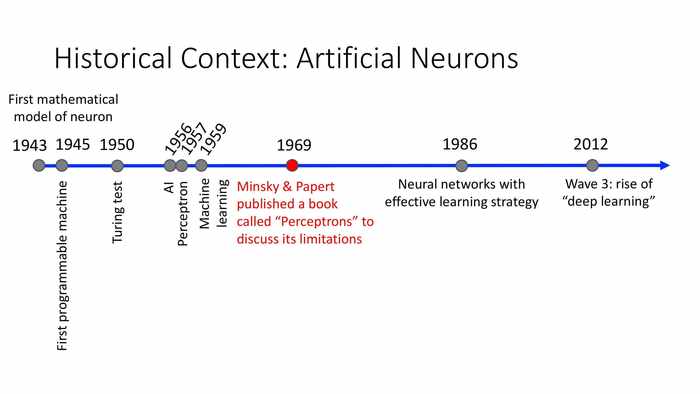
1969年，Minsky和Papert出版了一本名为《感知机》的书，来讨论这套数学模型的局限性。

(回顾：感知机的愿景)

（感知机是）[美国海军]预期中的电子计算机的胚胎，它将能够行走、谈话、看、写、自身重构以及意识到自身存在...[它]预期在一年内以10万美金的造价完成。

*上一篇的最后我们也总结了，一个简单的权重调整模型还完全达不到这个效果。

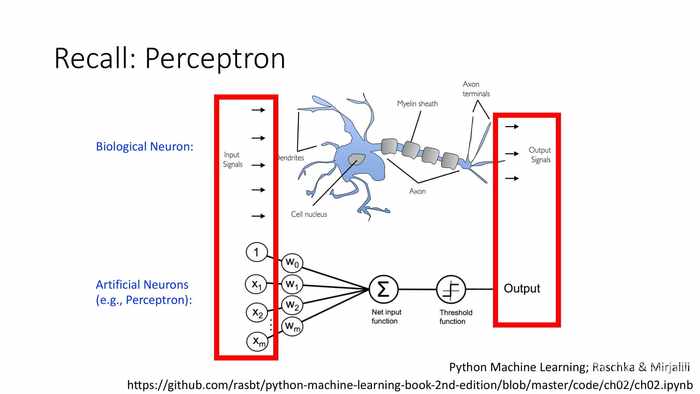(回顾：感知机)

*构建感知机的基本思想是模仿神经元，试图模拟其对于信号的接收、处理、激发、输出的过程。

(感知机的局限：异或问题)

输入：两个二元值x1和x2。

输出：当仅有一个输入等于1时，输出1；否则输出0。（*可以理解为对二元不相等的判断）

*按规则输出的结果如图。

*感知机的原理是二元空间划分（线性函数），而异或问题无法通过二元空间划分的方式来得到结果。

如果一个机器都无法解决异或问题，那它又如何能被称为“有意识”呢？

2 神经网络架构：隐藏层——Neural network architecture: hidden layers

*很自然的，引入多层结构就势在必行了。

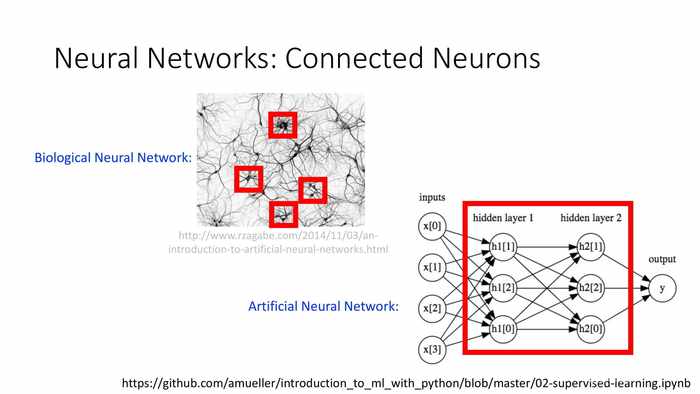(神经网络：连接的神经元)

*隐藏层的设计出发点就是模拟神经网络中神经元连接的形态。

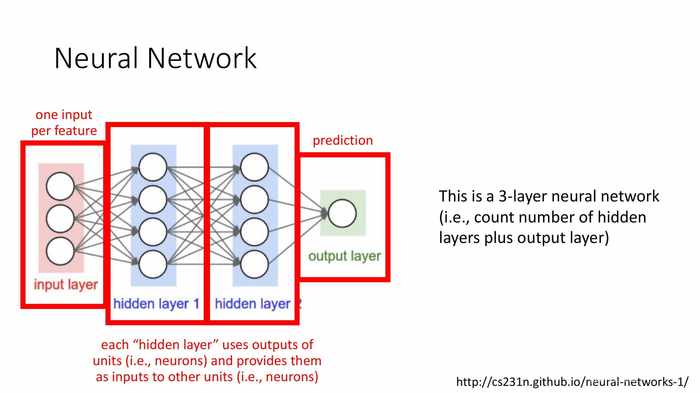(神经网络)

红色字部分，从左到右：

• 每个输入一个特征。
• 每个“隐藏层”使用单元（例如：神经元）的输出，并将其作为的输入传递给其它单元（例如：神经元）。
• 最终输出预测结果。

图中是一个3层的神经网络（统计隐藏层加输出层的总数）。

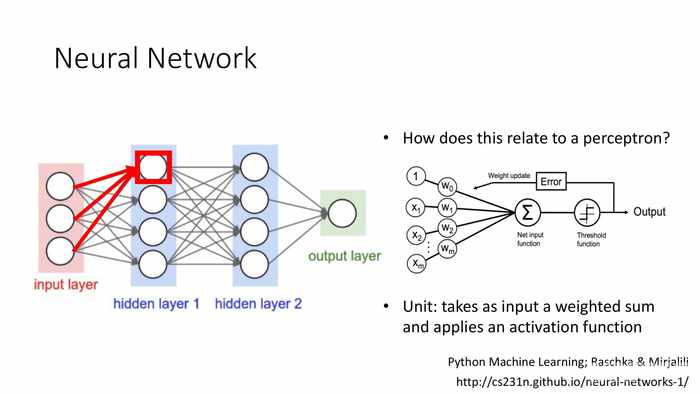
这一结构和感知机的联系是什么？

单元：接受一组权重和输入，并应用于激发函数。

*后面略去了3张相似的图，分别是输入给第1层的几个节点单元。

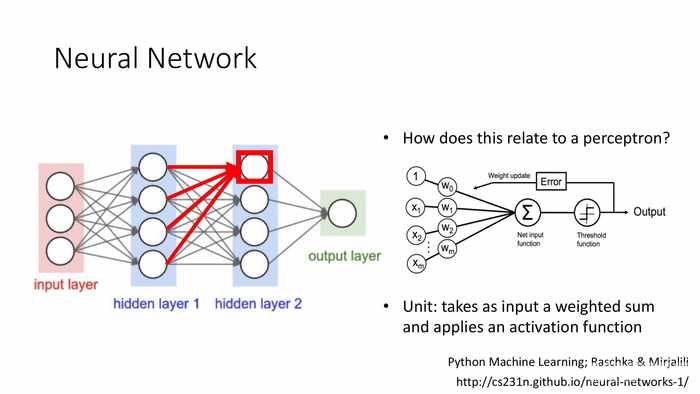
*第二层的类比，还是一样，包含输入来源和权重项。这部分和感知机同理。

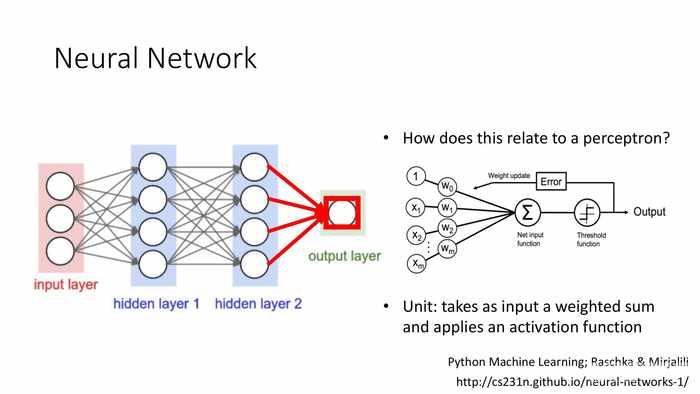
*最后是输入节点，4个输入来源和4个对应的权重项。

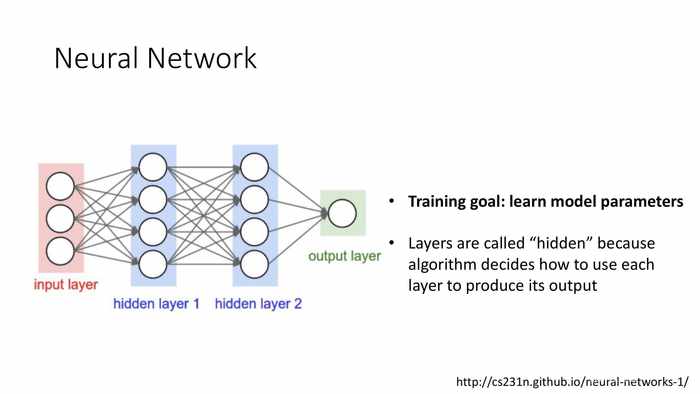
训练模型：学习模型参数。

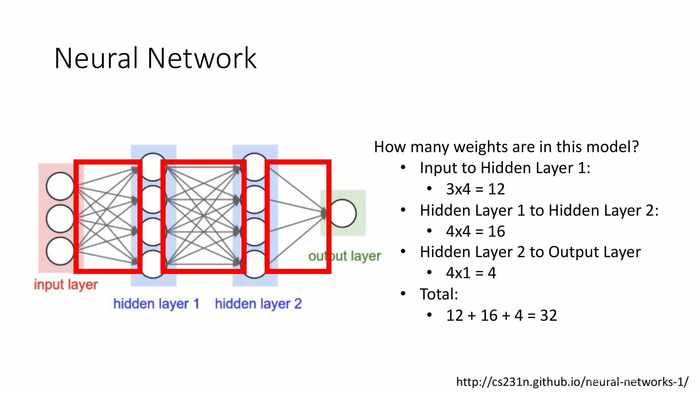
模型中总计有多少权重项？

• 输入给隐藏层1：3X4=12个
• 隐藏层1输入给隐藏层2：4X4=16个
• 隐藏层2给输出层：4X1=4
• 总计：12+16+4=32

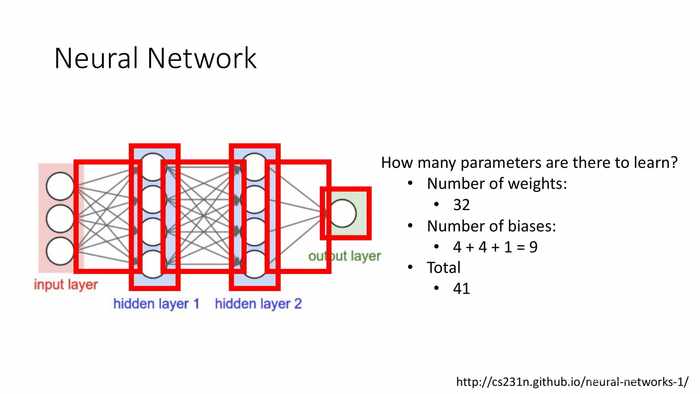
总共有多少待学习的参数？

• 权重数：32
• 偏移值：4+4+1=9
• 总计：41

*关于感知机的权重数和偏移值如何训练，可以参照上一篇。

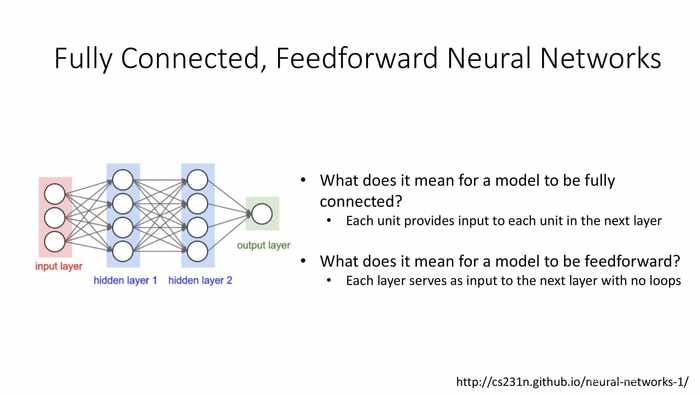(全连接的，前馈神经网络)

一个模型是“全连接”意味着什么？——每个单元（都）为下一层的各单元提供输入。

一个模型是“前馈”的意味着什么？——每一层都无循环地为下一层提供输入。

(仅隐藏层还不足以建模非线性函数)

核心观察：前馈神经网络只是连接在一起的函数。

*如图中的示例，3层的结构最终可以写成蓝框中的函数。

*而一个线性函数在任何深度都还是一个线性函数。（不足以解决异或等问题）

3 神经网络架构：激活函数——Neural network architecture: activation functions

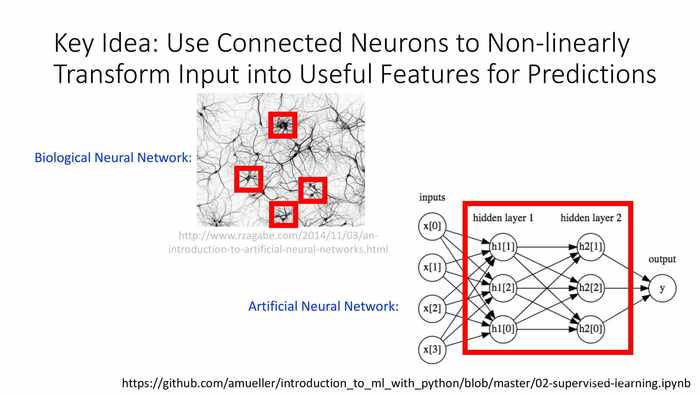
核心理念：使用连接的神经元，以非线性变换的方式输入有用的特征值，以用于预测。

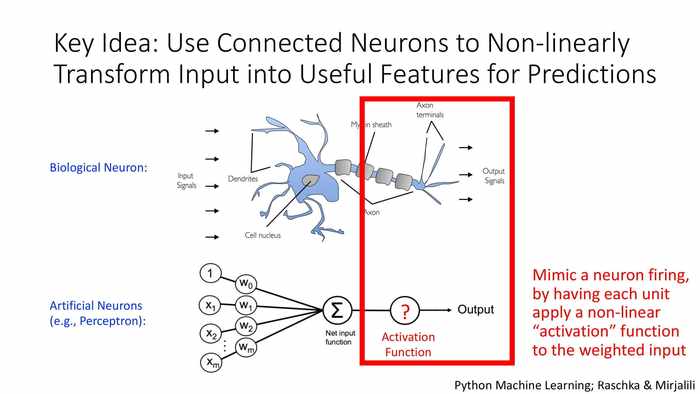
模拟神经元激活的过程，使每个计算单元的加权输入应用一个非线性的“激活”函数。

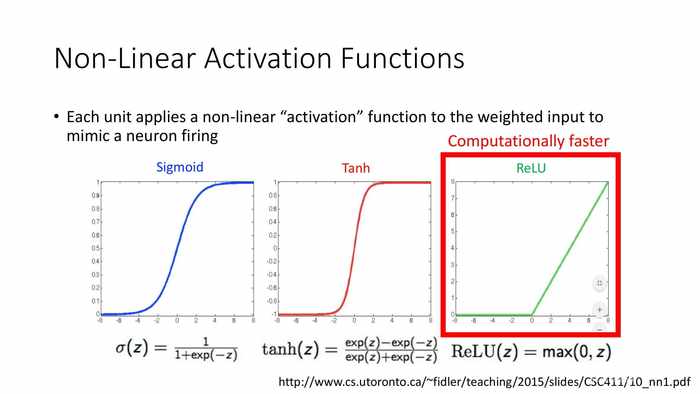(非线性激活函数)

*Sigmoid函数通常被称为S型函数或S型增长曲线。

*Tanh是双曲正切函数。

*ReLU是线性整流函数（Linear rectification function） 的缩写，又称为修正线性单元。它有着更快的计算速度——从各公式的区别可以看出（exp计算越多就越慢）。

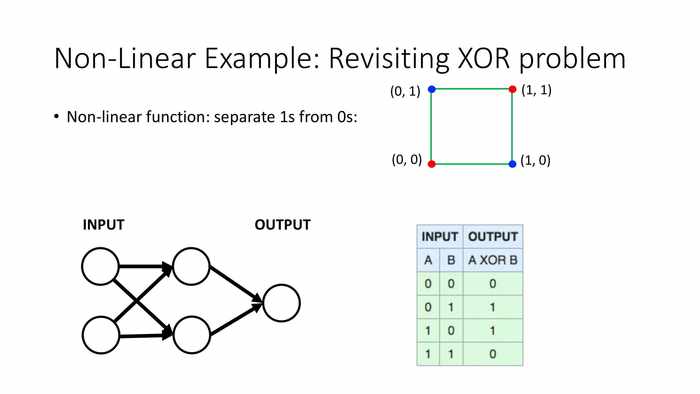(非线性的例子：重访异或问题)

非线性函数：将1从0中分离出来。

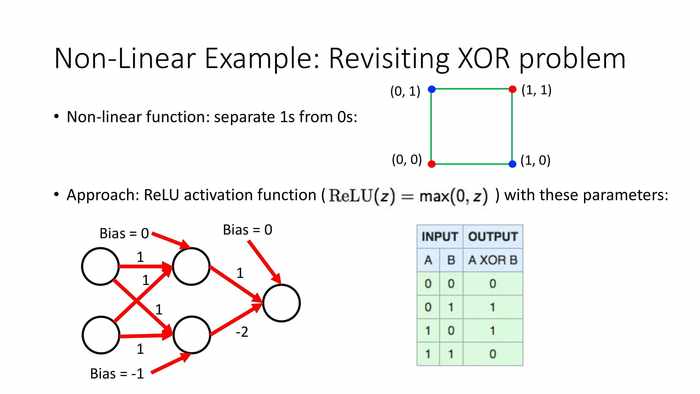
方法：使用如下参数的ReLU函数。（初始的权重值和偏移值如图，z对应计算过权重和之后的输入值）

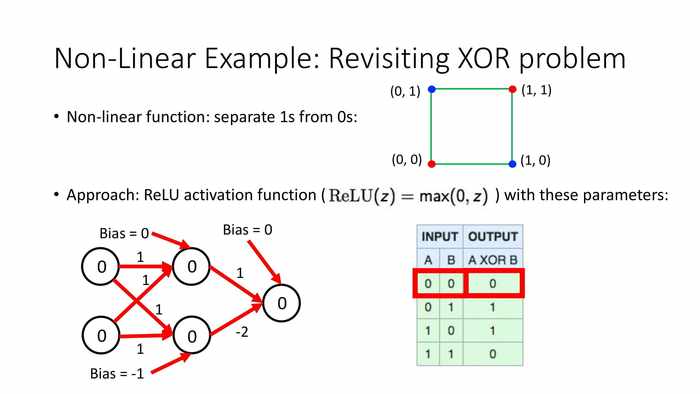
*当输入为0和0时，乘积都是0，max值也是0。最后输出0。

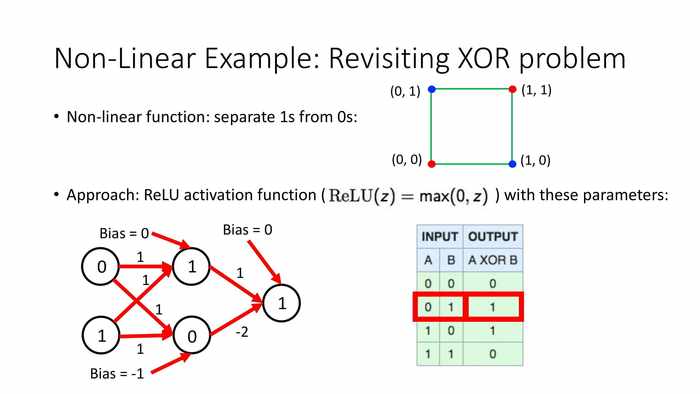
当输入0和1时，上方01+11+0=1，max(0,1)输出1；下方01+1*1-1=0，max(0,0)输出0；

总输出max(0,1)，输出1。

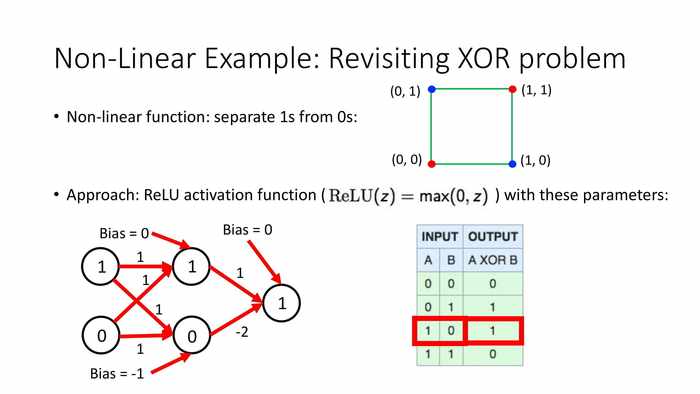
当输入1和0时，上方11+01+0=1，输出max(0,1)=1；下方11+0*1-1=0，输出max(0,0)=0；总输出max(0,1)=1。

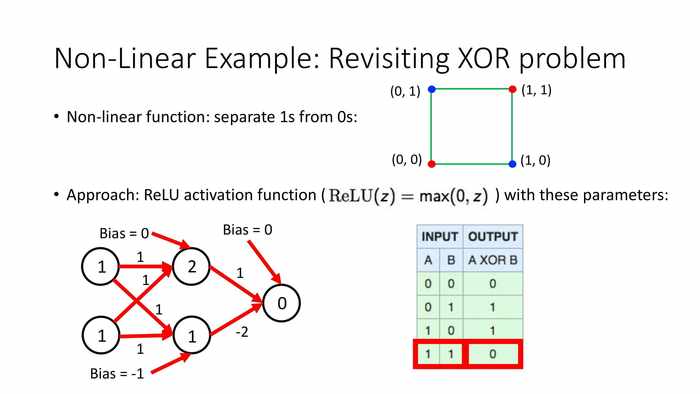
当输入1和1时，上方11+11+0=2，输出max(0,2)=2；下方11+1*1-1=1，输出max(0,1)=1；总输出max(0,0)=0。

（蓝字）神经网络可以用类似的数学建模方式来解决异或问题。

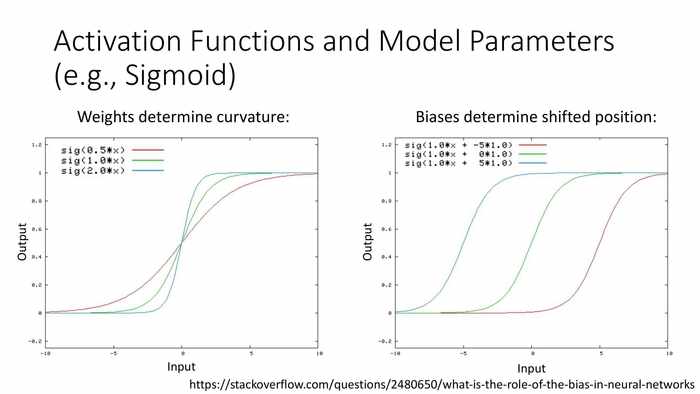(激活函数和建模参数（以Sigmoid曲线为例）)

（左图）权重决定曲率；（右图）偏移值决定相位。

*总的来说，建模异或计算是通过一组预先设计的激活函数的方式。

4 神经网络架构：输出单元——Neural network architecture: output units

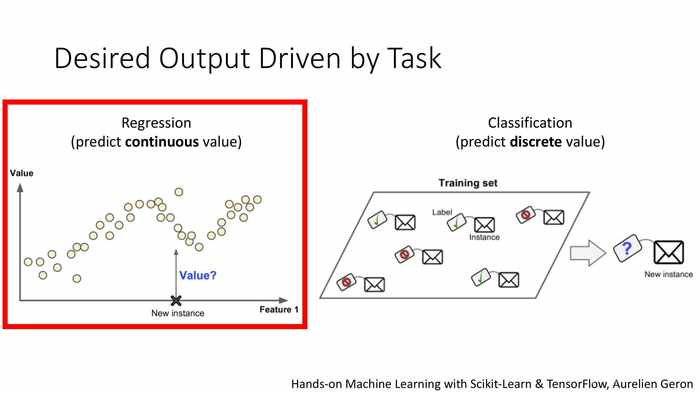(任务驱动的预期输出)

左图：回归，预测连续的值。

右图：分类，预测离散的值。

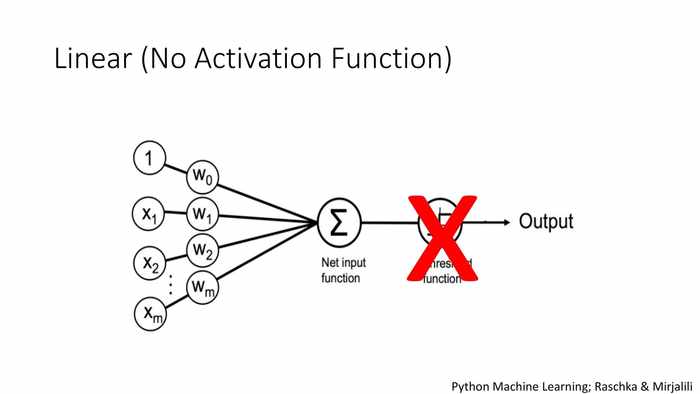(线性（非激活函数方式）)

*这里值输出值也不是直接线性输出，而是对于最终输入的值（分值）需要额外做一定的预判或处理。

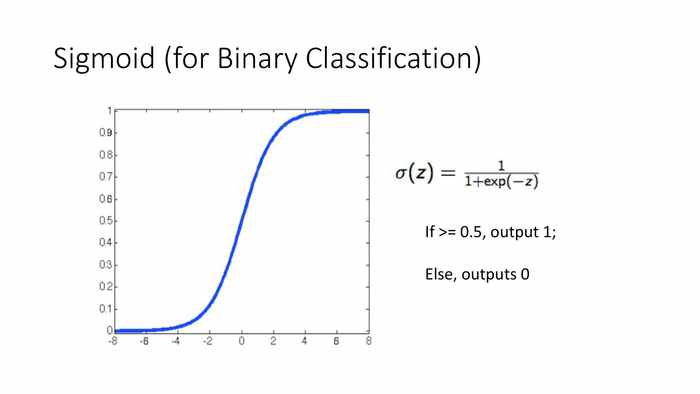(Sigmoid曲线（用于二元分类）)

*应用于二元分类时，这里对函数补充了逻辑分段，当大于0.5时，输出1；否则输出0。

(软上限（对于多类型分类）)

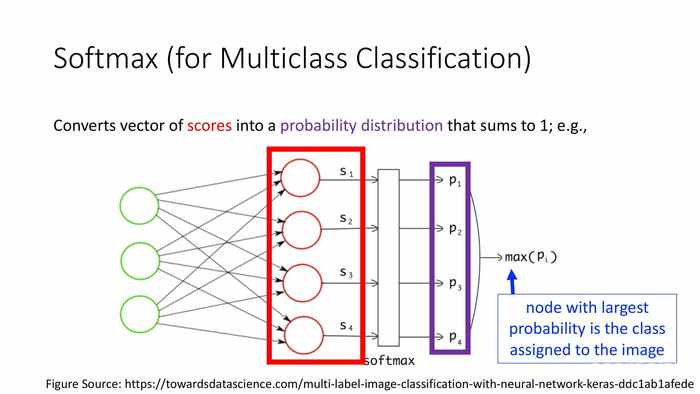
将分值向量转化为（总和为1的）概率分布。

（对于图像识别的例子）有着最大概率的值会被分派为图像的类型。

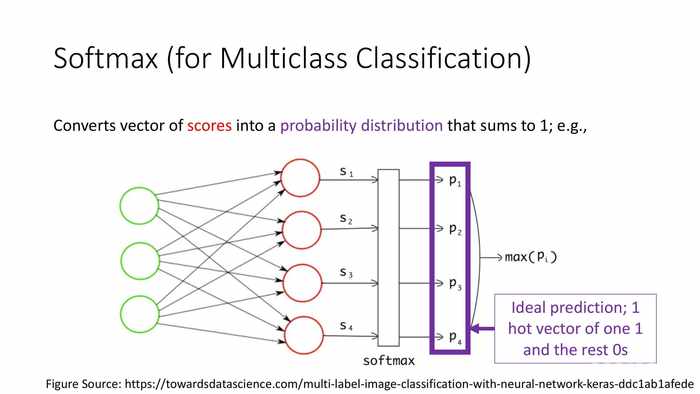
理想状态下，仅有一个概率为1的热向量，其它输入概率都为0。

（图中蓝字）在保持原始分值顺序的情况下处理负值；e使得负数分值变成略大于0，而正分值呈指数增长（使用e作为指数基，是因为它比其它值更利于训练时简化数学计算）。

*图中i代表样本的序号，K是类型数量（j是类型数量累加的下标）。除以框体中分母则是归一化计算的过程。

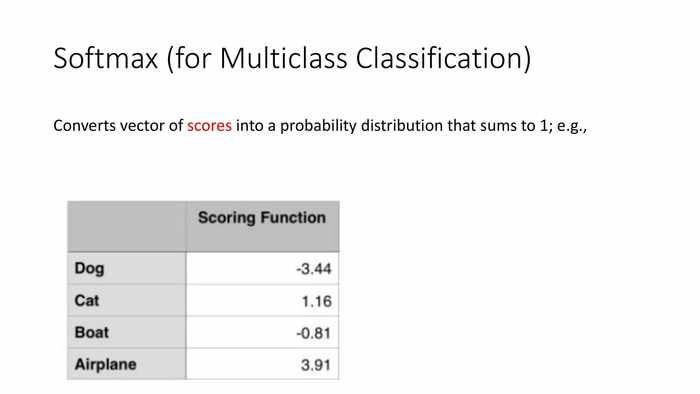
*这里是一组案例，通过打分函数得到的分值如图。

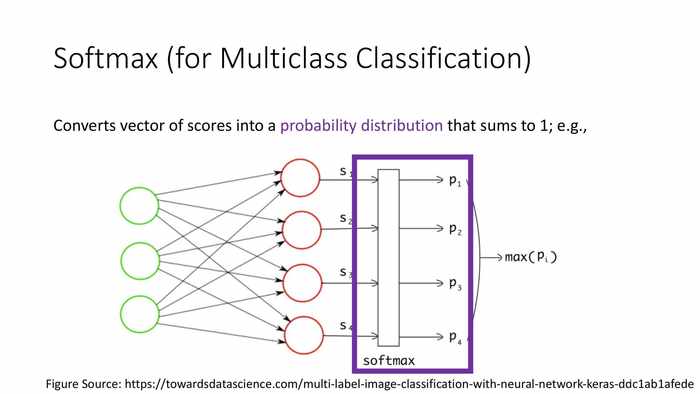
*首先对负值处理后输入各自的s，计算p值。

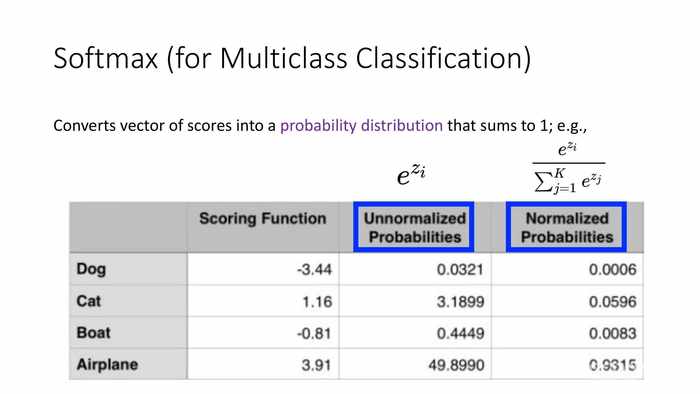
*图中展示了转化成概率分布的两种情况——非归一化的概率、和归一化的概率。

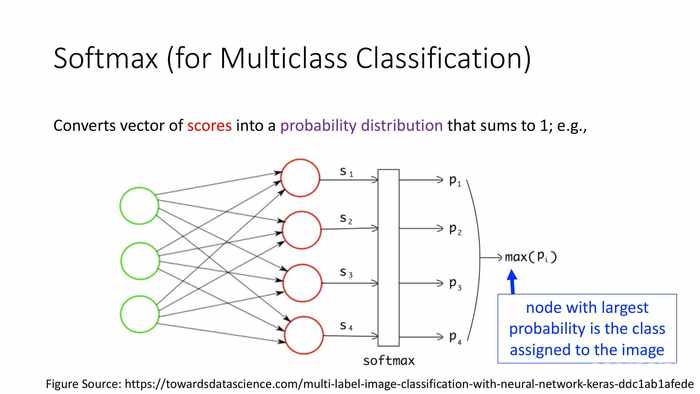
*这里软上限选择概率最高的类型。

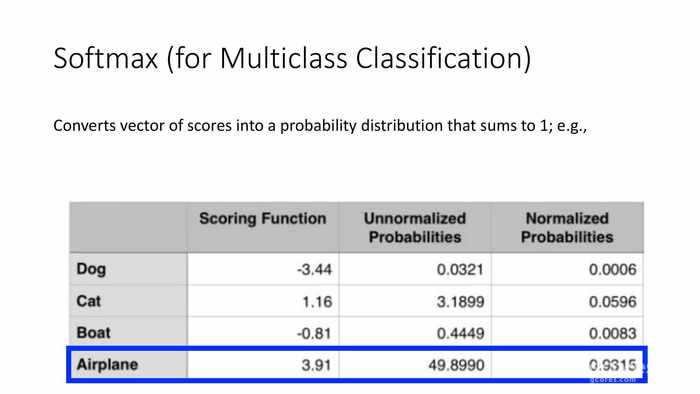
*所以图中的分类判定结果为Airplane——飞机。

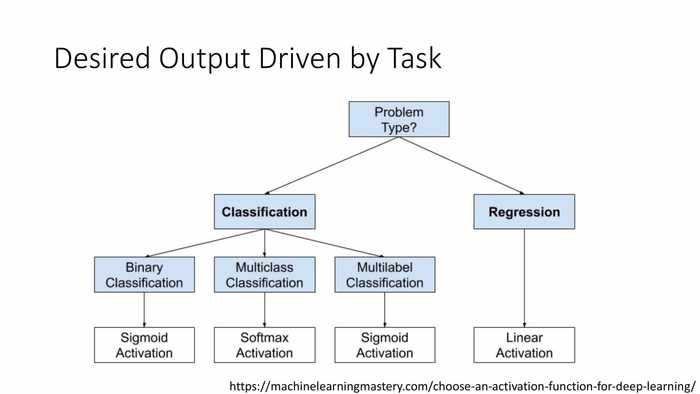
这里看一下树状分类图（从左到右、从上到下依次为）：

• 问题类型？分类、回归。
• 分类：二元分类——sigmoid函数激活、多类型分类——软上限激活、多标签分类——sigmoid函数激活。
• 回归——线性激活。

结语

从本篇可以看出，其实神经网络建模就是不断抽象各种数学模型以解决逻辑思考中会遇到的各种问题的过程。这次读到的内容不太涉及训练的过程，而是对预设的激活函数和输出函数有了更多的挖掘。

结合上一篇感知机（对应神经网络中的神经单元）的训练，至少我个人对于前馈式神经网络的基本原理和能解决的问题已经有了基本的理解。后续也会读到更多越来越复杂的结构，而“神经网络”这一概念会越来越接近最新的样子。

五一假期可能鸽一期，之后继续更新这个系列。

最后是资料链接：

NeuralNetworksAndDeepLearning-Spring2022/Lectures/03-Feedforward_NN.pdf