无论是制定预算、优化库存管理，还是探索新业务的潜力，时间序列预测都扮演着关键角色。本文将深入探讨时间序列预测的常见应用场景，介绍几种经典的时间序列模型（如移动平均、指数平滑、Holt-Winters、ARIMA和Prophet），并讲解如何评估模型效果，希望可以帮到大家。

上一篇Deepseek生成预测报告有点小激动，还没解释模型，现在补一下

1 什么场景下会使用到趋势预测？

业务场景还是挺多的，比如：

• 每年年末或年初，做预算规划或目标设定时，会根据历史基线、增长速度等给下一年定个目标值，有时会像《定个好基准》中所说参考环比同比来拍一个目标。
• 或者需要根据季节性、周期性特点，以及短期内的销售情况，对未来库存进行预估，更及时地进行备货调整。
• 或者未来想开拓一个新业务，预估未来市场有多大潜力空间。
• 又或者在推荐等模型优化时将预测值作为输入特征。

……

2 几个时间序列模型

在上一篇文章中实操了一下预测，但对这些模型还没做说明，接下来统一解释。

时间序列模型很重要的特点是，除时间外它只有一个变量，它所研究的是如何加工这一个变量，找到它随时间变化的特点，再进行预测，而没有通过其他相关数据辅助预测。举例来说，预测未来一个季度的销量，变量只有历史的销量，而不含有流量、转化率等数据。

适用于中短期

1. 移动平均

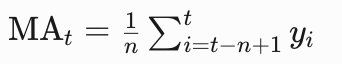
看公式很容易理解，间隔为n的时间窗口内的平均值，该值可作为T+1的预估值，适用场景通常为趋势稳定的数据，如果数据有周期性，会出现预测峰谷值同实际错位的情况。

2. 简单指数平滑

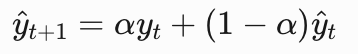
y^为预测值，y为实际值，α为平滑系数，范围（0，1），α越大近期更敏，感适合波动较大的数据，反之越平滑适合稳定趋势。T+1的预测值，为t天实际值和预测值的加权所得。3. Holt-Winters

包含水平平滑、趋势平滑、季节性平滑。

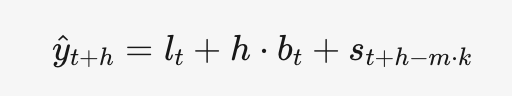
水平平滑

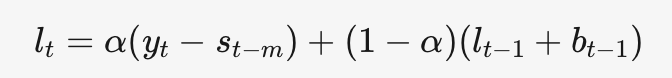趋势平滑

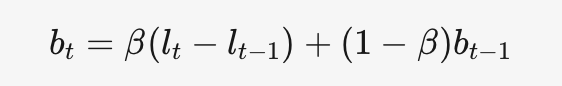
季节性平滑

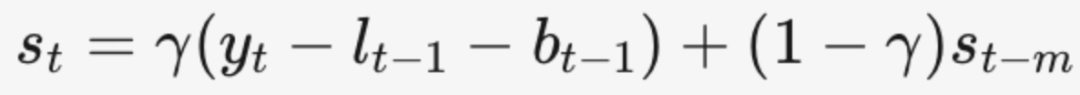
几个参数：

• St：当前季节分
• m：季节周期（如m=12为以月为周期，12个月为一个循环）
• α、β、γ分别为水平、趋势、季节性平滑参数，范围（0，1）
• h：步长，预测是跨几个步长进行预测，一般是1
• k=(h-1)/m+1

有点抽象，举个例子说明，假如如下对应每个季度的商品销售量，现在想要预测2025Q1(t=9)的销量

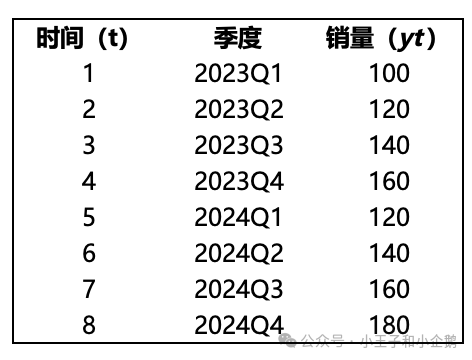
假设参数设定：α=0.3（水平） β=0.2（趋势） γ=0.1（季节性），季节周期：m=4

初始化预测参数：

• l4=（100+120+140+160）/4=130，即前4个季度的平均值，
• b4=平均季度增长=（120-100）+（140-120）+（160-140）/3=6.67
• s1=100-130=-30，s2=120-130=-10，s3=140-130=10，s4=160-130=30

预测2024Q1(t=5)：y5预估=l4+b4+s5-4=130+6.67-30=106.67，实际y5=120

更新预测参数，即t=5对应的预估值，

• l5=0.3（120+30）+0.7（130+6.67）=140.67
• b5=0.2（140.67-130）+0.8*6.67=7.47
• s5=0.1（120-130-6.67）+0.9（-30）=-28.67

以此类推，可得到y9预估值=l8+1b8+s9-42=149.63

虽然手动算麻烦一点，但以上这两种方式，确实可以通过计算看到数据和趋势变化如何产生。

适用于中长期

接下来要聊的两种方法，就不足以通过手动计算了。

4. ARIMA(p,d,q)。时间序列预测很古典和著名的方法。

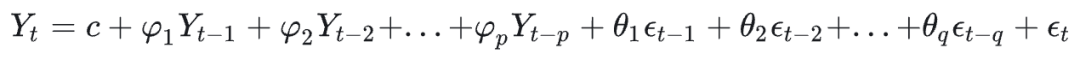
模型是由三部分组成：

自回归部分AR

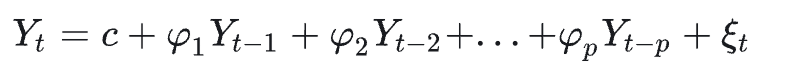
p为参数，核心解决的是预测未来的数据，应该选历史多少个时间点的数据更好，最远的时间是t-p，因此p为参数。

移动平均部分MA

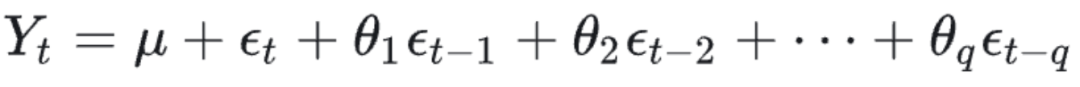
q为参数，要解决的是y实际值和y预测值之间的差，选择历史上多少个时间点更好，最远时间为t-q，因此q为参数。

差分部分，d为参数，要解决的是 yt-yt-1 这样做几阶差分更好，为的是把非平稳的数据转换为平稳数据。

先通过ADF检验对d进行差分检验（与统计临界值对比），在通过ACF(自相关函数)和PACF(偏自相关函数)分别对p和q进行检验，通过AIC和BIC对模型复杂性评估后可得到更为合理的p、q值。

5. Prophet。时间序列进化到Prophet，操作更友好了。

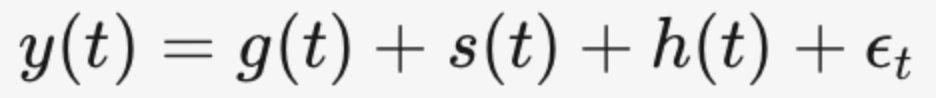
模型是由三个小模型组成，ϵt 为误差项

• g(t)：增长和分段线性模型（线性或者逻辑回归函数）
• s(t)：周期性和季节性模型（正弦和余弦组合函数）
• h(t)：节假日或特殊事件模型（线性函数） 该模型很好理解，且命中了趋势预测里经常要思考的几个问题：如果趋势有上升和下降几段趋势怎么办？周期性的数据并非完全自然周期怎么办？遇上突发事件出现某个点异常怎么办？过往的时间序列模型很难进行拟合和描述，不过Prophet解决了这个问题。

这里对具体公式不详细展开，感兴趣可在参考资料里了解，这里主要介绍模型参数的作用，对实操会更有帮助。

• growth（增长函数类型）：linear（默认）：线性增长，适用于无明确上限的趋势（如销售额），logistic：逻辑回归增长，适用于有增长上限的场景（如用户数）；
• changepoint_prior_scale（变点灵敏度）：0.001~0.5（默认 0.05），若预测结果过于平滑（欠拟合）增大该值，若预测结果波动剧烈（过拟合），减小该值；
• n_changepoints（变点数量）：25（均匀分布在时间序列前80%区间），越大将趋势变化切分越多；
• seasonality_prior_scale（季节性强度）：0.01~10（默认10），值越大季节性波动越大；
• add_seasonality（傅里叶阶数）：name=’yearly’, period=365.25, fourier_order=12，fourier_order越大阶数越高拟合越复杂，name对应的是yearly，weekly，daily或者命名一个，period写对应周期；
• holidays_prior_scale（节假日效应强度）：0.01~10（默认 10），值越大节假日波动越强。
• 节假日窗口，比如双11大促:

holidays_df = pd.DataFrame({

‘holiday’: ‘promo’,

‘ds’: pd.to_datetime([‘2022-11-11’, ‘2023-11-11’, ‘2024-11-11’]),

‘lower_window’: -30, #双11前30天

‘upper_window’: 2  #双11后2天

})

后边也有新的升级 Neural Prophet，如果感兴趣也可以再查找了解。

3 如何评估模型效果

预测时数据会切分成两部分，训练集和测试集，评估模型效果简单来讲就是拿训练集得到模型，后再去预测测试集对应的数值，把测试集的真实结果同预测结果比对，差异越小说明预测越准确，但也要兼顾鲁棒性，注意不要过拟合。

几个线性模型评价模型准确度的指标和计算公式如下，比较简单就不做过多解释了。

MAE 平均绝对误差

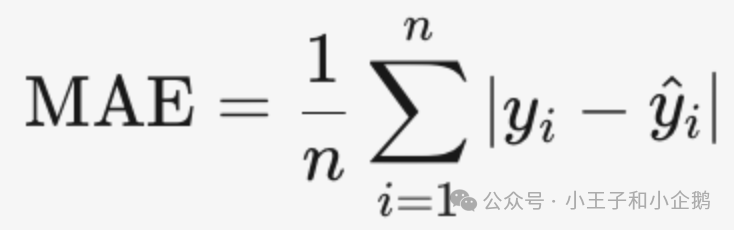
RMSE 均方根误差

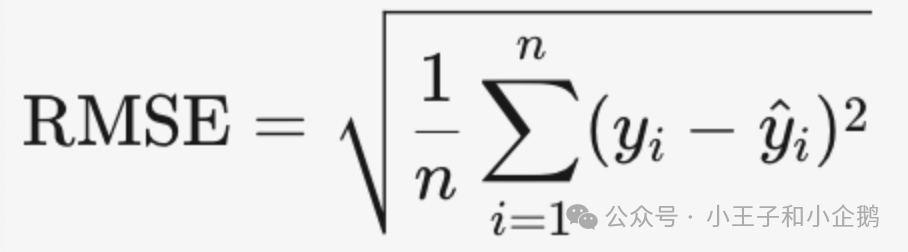
MAPE 平均绝对百分比误差（使用时不能有0，且去量纲可比较不同数据集）

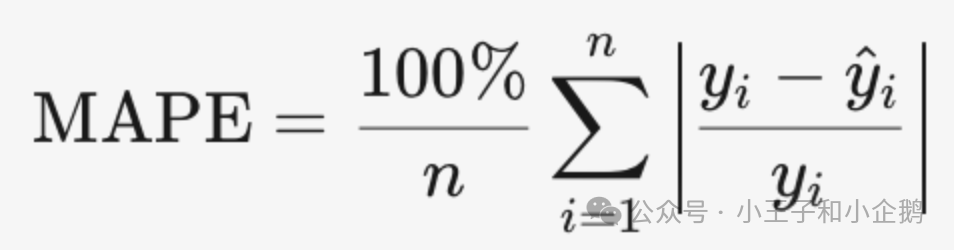
参考资料

知乎文章《时间序列原理篇之Facebook Prophet算法》

知乎文章《时间序列模型(四)：ARIMA模型》

本文由人人都是产品经理作者【小王子和小企鹅】，微信公众号：【小王子和小企鹅】，原创/授权 发布于人人都是产品经理，未经许可，禁止转载。

题图来自Unsplash，基于 CC0 协议。